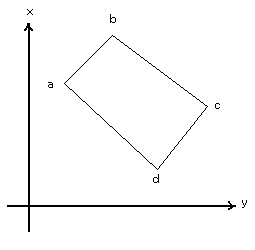
| まず、4点が右図のようにあるものとして、それぞれの座標値は以下のとおりとする。 a(x1,y1) b(x2,y2) c(x3,y3) d(x4,y4) 面積を求めるためにそれぞれを分割して考える。 それぞれの点からy軸上に垂線をおろし、隣り合った点との垂線で囲まれた部分(台形になる)の面積(正負の区別はする)を合計することで、四角形abcdの面積を求めようとする方法である。 |
 |
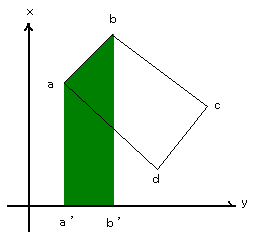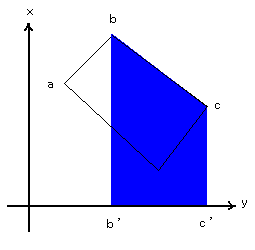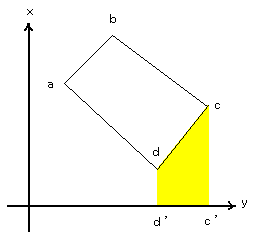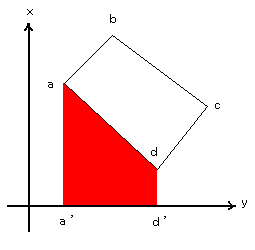
| まず、一つ目の台形として右の緑色の部分を考える。 四角形abb'a'の面積S1は、台形の面積を求める公式から次のように表せる。 台形の面積=(上底+下底)×高さ÷2 S1=(x2+x1)×(y2−y1)÷2 同様にして、 S2=(x3+x2)×(y3−y2)÷2 S3=(x4+x3)×(y4−y3)÷2 S4=(x1+x4)×(y1−y4)÷2 となる。 ここで、S2は青色の部分、S3は黄色の部分、S4は赤色の部分の面積を算出しているものである |
 |
| さて、ここで考えて見ると、なぜS1からS4の合計が四角形abcdの面積になるのであろうか。 その秘密は、高さの部分にあたる計算式に秘密がある。 それは、 S1における高さの部分(y2−y1)及びS2における高さの部分(y3−y2)が正 S3における高さの部分(y4−y3)及びS4における高さの部分(y1−y4)が負 となることである。 つまりは、四角形の頂点をa→b→c→d→aと回ることでa→b→cまでは正の向き、c→d→aまでは負の向きとなり、結果正の向きのときの面積は求めようとしている図形を含むy座標までの面積を求め、負の向きのときの面積は求めようとしている図形を含まないy座標までの面積を求めていることとなる。 そしてそれを全て加算することで、求める図形の面積を算出しているのである。 では、それぞれの算式がもう少しまとめられないか考えて見ることにしよう。 |
|